Heuristic

Zebra finches use a “critic” in the brain to differentiate between the rhythm of songs of other birds and, through this, learn songs.

Like the ebb and flow of the ocean, 

A rhythm emerges from the pen,

I capture it, imagine it,

before it disappears. 

Appropriate rhythm in writing means making sense of the relation between words and phrases. Stress, repetition, fluctuation, rhyme, meter, pattern, juxtaposition, and harmony all come together. These form the aesthetic and intellectual properties of rhythm. For a philosopher studying semantics or neuroscientist uncovering our nature, rhythm poses challenges. I’ve written on the subject with respect to symmetry. Let’s delve into rhythm’s secrets philosophically, mathematically, and scientifically.

Through much of my scientific writing, I pay close attention to how lengthy my sentences are. Too many long sentences at once can lose the reader in monotonous, cumbersome passages. I especially fall into this trap with description and exposition.  Long sentences bore the reader. Short, astute sentences can feel abrasive and clumsy. We alternate between the brevity of Twitter to the nuance of academic prose. it’s easy to succumb to habits and forget about the appropriate rhythm with which to write. Rhythm is both something we plan in advance and  re-evaluate through reflection and speculation.

In the realm of aesthetics, philosophers have debated the role of rhythm since the Classical era. In Book III of Plato’s The Republic, Socrates clarified that rhythm and meter are what separate poetry from pure prose. Pre-Medieval philosopher St. Augustine developed a theory of aesthetics based on ideas of rhythm in De Musica. In congruence with the theologian’s religious beliefs, God is the origin of rhythm. We discover these mathematical truths, pre-determined by God, of rhythm. It’s like how Plato believed humans collectively remembered them.

Emerson’s poem “Merlin” showed the use of rhyme and meter to create rhythm. Particularly the lines that moved back and forth between his own sensations and the way to craft meters of poetry from them showed this. Emerson in this section, showed how the rhyme fit so naturally that it seems like part of human prose. Socrates’ idea of rhyme and meter separate prose from poetry  lets Emerson use this distilled rhythm.

Thy trivial harp will never please

Or fill my craving ear;

Its chords should ring as blows the breeze,

Free, peremptory, clear.

No jingling serenader’s art,

Nor tinkle of piano strings,

Can make the wild blood start

In its mystic springs.

We teach ourselves rules and tips on creating great writing to take into account the effect of the rhythm on the piece. To imagine and care for these aspects of the reader gives the writing a property only observed at a scale larger than individual words. Rhythm comes from how words interact with each other, yet remains limited by our conventions of writing. It emerges when you take a step back from your computer screen and look at the whole picture. Rhythm is this frequency. Time itself limits these perceptions as we read. As such, it reveals deeper features of our subjective perceptions, such as the stress, intonation, and tempo of speech itself.  Yet we speak of it as something deeper than the combined intrinsic content of words themselves. In this sense, it’s like an emergent phenomena, much like evolution selecting certain genetic traits.

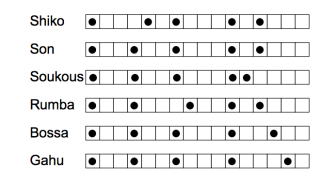What makes these six clave patterns fundamental are that they reveal maximally even rhythms and maximum sum of pairwise distances between the points as vertices on a tetrahedron.

In a scientific context, we rely on our empirical observations of rhythm to determine higher truths of rhythm.  Canadian computer scientist Godfried Toussaint finds this connection between shape and musical rhythm. Due to the evenness of six musical clave patterns, they have mathematical significance. That a mathematical algorithm could generate music raises questions about what is music. It raises questions as what sort of mathematical or empirical technique governs what “good” rhythm sounds like.

Placing the six intervals in histogram form reveal patterns among themselves that may dictate the nature of rhythm as a whole.

We can find fundamental features among strings of numbers such that the patterns of these features give rise to Euclidean rhythms. These are rhythms created by Euclidean distance, or the straight line distance between the points when arranged in a circle. The numbers show the span between the beginning of successive notes and, thus, represent the simplest way to represent rhythm. This needs much more empirical evidence before showings its truth in all music. Toussaint’s claim that Euclidean rhythms that are reverse Euclidean strings appear to have a much wider appeal. French mathematician Jean-Paul Allouche showed these strings of numbers are like combinations of words. Other mathematicians and computer scientists have developed Euclidean rhythms from Euclidean strings. Toussaint argues that the Euclidean algorithm finds the greatest common divisor of two numbers. It can generate rhythm timelines by using the two numbers as an input to the Euclidean algorithm. The two numbers would dictate the beginning of each note in the rhythm and the span between notes. 

In the field of cognitive neuroscience, we can study the ways humans and other organisms produce and  test rhythms. Computational neuroscientists Kenji Doya and Terrence J. Sejnowski discovered a “critic” within the zebra finch brain. It lets the finch to differentiate between songs. NMDA receptors, a specific method of chemical signaling in nerve cells, activate to let bird to learn the “correct” song. Scientists Philipp Norton and Constance Scharff found patterns between the nerve and muscle cells. They corresponded with elements of notes and duration of the notes themselves. This is like Toussaint’s study of the beginning of each note determining rhythm. It includes the span between them, both fundamental components of rhythm. This research holds value for finding similar discoveries in the human basis of rhythm as well.

Much the same way a poet translates nature into word, a scientist would find quantifiable metrics of music. They may raise questions for musicology, geometry, and, with enough empirical evidence, neuroscience. Now take a deep breath and let the waves beat upon the seashore. Detect the rhythm and move along like before. 

Sources

Doya, Kenji & Terrence J. Sejnowski (1999). The New Cognitive Neurosciences. II. MIT Press. pp. 469–482.

G. T. Toussaint, “The Euclidean algorithm generates traditional musical rhythms“, Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science, Banff, Alberta, Canada, July 31 to August 3, 2005, pp. 47–56.

Norton, Philipp & Constance Scharff (2016). “Bird Song Metronomics”: Isochronous Organization of Zebra Finch Song Rhythm. Frontiers in Neuroscience.